さて,この実験によって,面白いことが明らかになった.安定不動点に落ちつくグラフを見ると,われわれはこの現象が,なんらかの法則によって支配されているのではないか,と予想することが出来る.結果が秩序的ならば,それを生じさせる整合的な原因としての法則がその背後に潜んでいるのではないか,と推測するわけである.
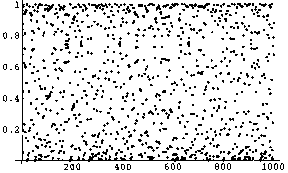
ところが,a=4のピュアカオス状態のグラフを見ると,これがなんらかの単純で整合的な法則に従う現象だとは到底考えることができない[★7].しかし,この実験で示したように,あの全くの無秩序状態は,Y=4X (1−X )という単純な方程式を繰り返し適用することによって成立してきているわけである.あのランダムなグラフを見る限り,これが決定論的に一つの法則から導きだされた結果だと知らなければ,あの無数のランダムな点の間の関係を探ろう,という気さえ起こらないだろう.
ここでは,単純な結果は単純な原因から,複雑な結果は複雑な原因から,という従来の思考法が,大きく問い直されているわけである.
そして,この知見は,次のような誘惑を発生させる.現実にあるきわめて非周期的でランダムな現象の背後に,もしかしたら,統一的で単純な法則が潜んでいるのではないだろうか,と.
株価の変動,経済景気変動,非周期的な地震の発生,気象現象,心臓の不整脈,等々,複雑系の背後に単純な法則が潜んでいるのではないか.そして,その法則を知ることで,それらの複雑系の構造を理解し,予知することができるのではないか,と.
一般に,カオス問題が語られる時には,この複雑系から単純なものへ,という観点で多く語られる.しかし,この方向でのカオス研究は,その主張は,常に蓋然性に留まらざるをえない.この複雑系はカオス現象かもしれない,と.
マンデルブローは,現在の幾何学と物理学との関係をめぐる問題において,カオス論には二つの方向があると語っている[★8].
1)単純な物理系で決定論的法則にしたがっているのに,予測不能な振る舞いが発生するという側面.
2)複雑で不規則な現象を数学的に表わそうとする側面.
この第二のアポステリオリな道は,カオス研究の醍醐味ではあるが,まずもって明らかにされなければならないのは,アプリオリな道,つまり,単純なものから複雑なものへ,という第一の道を確実な形で見定めておくことだと思われる.そうでないと,カオス研究は,文字通りカオス的状態へと退化してしまうだろう.
| 
