
| InterCommunication No.15 1996 |
 |
Monograph |
さて,X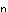 を,X を,X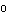 とaの関数として明示する{n年後の電子バッタの数を,初年度のバッタの数と繁殖率によって表わす}公式を導くことは原理的には可能である. とaの関数として明示する{n年後の電子バッタの数を,初年度のバッタの数と繁殖率によって表わす}公式を導くことは原理的には可能である.X 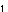 =aX =aX 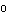 (1−X (1−X 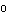 ) )X 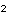 =a・aX =a・aX 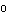 (1−X (1−X 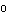 ){1−aX ){1−aX 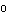 (1−X (1−X 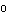 )} )}このような方式では,式は急速に,長く難解なものとなっていく.X 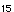 では,約1冊の本の長さとなり,X では,約1冊の本の長さとなり,X 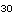 {30年後の電子バッタの数}では,ある資料によれば,「イギリスの国立図書館の蔵書分の長さ」となる.ここではその実感を掴むために,S・ウルフラムのソフトウェアシステムMathematicaを使用して,例示してみよう[★5]. {30年後の電子バッタの数}では,ある資料によれば,「イギリスの国立図書館の蔵書分の長さ」となる.ここではその実感を掴むために,S・ウルフラムのソフトウェアシステムMathematicaを使用して,例示してみよう[★5].X 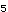 ,X ,X 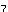 ,X ,X 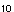 となるにしたがって,まさに爆発的に長くなり,X となるにしたがって,まさに爆発的に長くなり,X 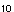 では,式がA4で10頁の長さとなった.100回繰り返して得られる値X では,式がA4で10頁の長さとなった.100回繰り返して得られる値X 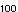 {100年後の電子バッタの数}は,公式で書こうとすれば,まさに天文学的な長さの式となってしまうだろう. {100年後の電子バッタの数}は,公式で書こうとすれば,まさに天文学的な長さの式となってしまうだろう.したがって,原理的には,X 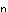 は初期値と定数aによって決定されている(はずである){何年後の電子バッタの生息数であろうとも,それは繁殖率と初年度のバッタの数によってあらかじめ決定されている}が,現実的には,逐次的に解を確かめていくしかない.次々具体的に代入していくのならば,保持すべきは,過去の全歴史ではなく,一つ前のX の値だけでよいからである. は初期値と定数aによって決定されている(はずである){何年後の電子バッタの生息数であろうとも,それは繁殖率と初年度のバッタの数によってあらかじめ決定されている}が,現実的には,逐次的に解を確かめていくしかない.次々具体的に代入していくのならば,保持すべきは,過去の全歴史ではなく,一つ前のX の値だけでよいからである.さて,逐次計算は,コンピュータのもっとも得意とするところである.再びMathematicaを使って実験してみよう.例えば,a=2, X 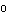 =0.4 としてそれを20回繰り返し行なう{繁殖率2で,初めのバッタの数が4000匹だとして,20年後までのバッタの数を求める}と結果は次のようになる. =0.4 としてそれを20回繰り返し行なう{繁殖率2で,初めのバッタの数が4000匹だとして,20年後までのバッタの数を求める}と結果は次のようになる.0.4, 0.48, 0.4992, 0.499999, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5, 0.5 {電子バッタの数は,始め4000匹で,翌年が4800匹,……となって,数年後からは,毎年5000匹に安定したまま,ずっとこの数をとり続ける.} 興味深いことに,a=2{繁殖率が2}の場合は,初期値にどんな値をとっても,最終的には0.5{5000匹}で安定する. ちなみに,初期値を 0.1と0.8で試してみよう. X 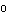 =0.1 の場合{最初,1000匹いる場合} =0.1 の場合{最初,1000匹いる場合}0.1, 0.18, 0.2952, 0.416114, 0.485926, 0.499604, 0.5, 0.5, 0.5, ...... X 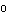 =0.8 の場合{最初,8000匹いる場合} =0.8 の場合{最初,8000匹いる場合}0.8, 0.32, 0.4352, 0.491602, 0.499859, 0.5, 0.5, 0.5, ……
ところで,この方程式の振る舞いは,定数aの値,大まかに分ければ,a<1,1<a<3,3<a<4のそれぞれで,異なった振る舞いをする{バッタの繁殖率,つまり1匹あたり,次の年に何匹残すか,の値で,バッタの年毎の生息数の変化はさまざまな形を取る}.
|